Cryptographie pour les néophytes : le chiffrement
Vous avez toujours rêver de comprendre les subtilités des algorithmes de chiffrement mais vous collectionniez les 5/20 en math ? Cet article est pour vous ! Nous y verrons le concept général de cryptographie symétrique et nous plongerons ensuite dans le détail. Il y en aura pour tous les goûts ! Il est tout de même préférable d’être passé par les fondamentaux pour bien comprendre les enjeux du chiffrement.
“La symétrie” en deux mots !
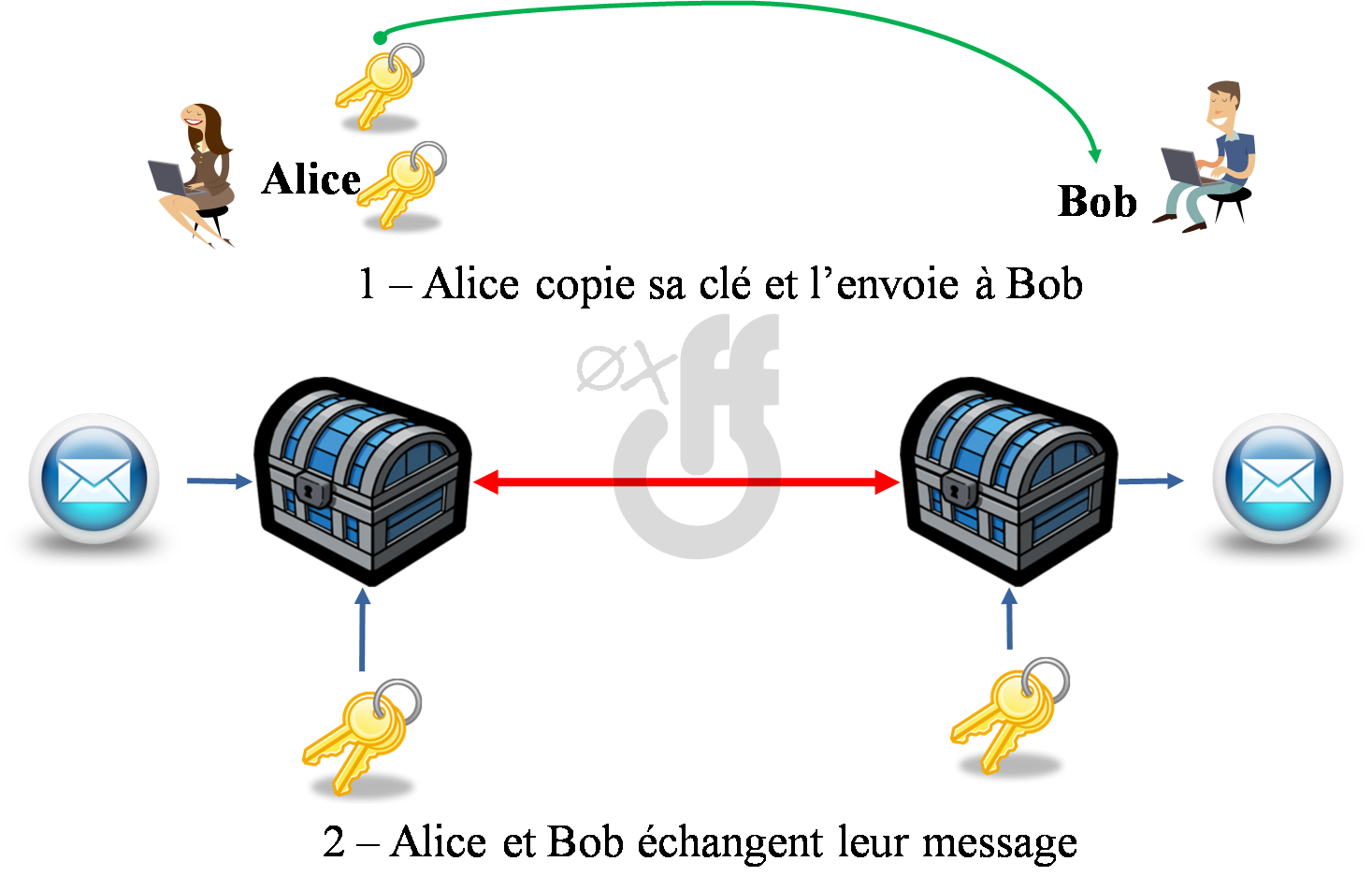
Et bien c’est très simple ! Envoyer un message chiffré à quelqu’un revient à envoyer votre message en clair dans un gros coffre que vous fermez avec un cadenas dont seuls vous et votre correspondant possédez une clé.
Plus votre coffre est solide et plus votre message est en sécurité, logique. Voilà à quelle notion renvoie le terme de chiffrement symétrique. Efficace non ?
Et dans le détail ?…
Ah je vous retrouve, animés que vous êtes par cette curiosité bénéfique ! Et bien dans le détail, il nous faut considérer trois choses :
- Les exigences d’un algorithme de chiffrement
- Le fonctionnement d’un algorithme de chiffrement
- Les types d’algorithme par bloc et par flot
Les exigences
Les exigences, ce sont les règles fondamentales que doivent respecter les algorithmes de chiffrement pour être considérés comme “sûrs”. Ces 3 principes sont la ligne directrice d’un cryptosystème… Je vais vous les présenter, on ne sait jamais vous voudrez peut être crâner partager ce savoir avec vos collègues pendant la pause café, tout à vous, Joie !
1 – Principe de Shannon
L’ordre de K est supérieur ou égal à l’ordre de C qui est supérieur ou égal à l’ordre de M
- K = groupe fini pour les clés,
- C = groupe fini pour les messages chiffrés,
- M = groupe fini pour les messages en clairs.
Nous l’avons survolé dans les fondamentaux mais je pense qu’il est intéressant de connaître l’énoncé de ce principe dans sa totalité. La grande idée est “On utilise une et une seule clé par message“.
2 – Principe d’entropie forte
La plus petite modification du clair entraîne une modification d’une grande partie du chiffré voir de sa totalité.
L’objectif est de ne pas pouvoir déduire du message chiffré, le message en clair ou la clé secrète… Il y a deux fonctions fondamentales pour assurer ce principe : la substitution et la permutation.
La substitution c’est le fait de remplacer un alphabet par un autre. On peut citer l’exemple du chiffre de César :
A B C D E F G H I J...X Y Z | | | | | | | | | | | | | D E F G H I J K L M...A B C
La permutation c’est le fait de mélanger les blocs de lettres :
Je suis un poisson Su jeun is isponso
3 – Principe de Kerckhoffs
Seule la clé doit être considérée comme secrète, l’algorithme est un élément publique.
Cela permet d’éviter toute fausse protection par obfuscation, justifiée par cette réflexion un peu simpliste “S’ils ne connaissent pas l’algorithme, ils ne trouveront jamais comment déchiffrer nos messages. Héhé on est trop fort.“. L’histoire nous apprend, parfois douloureusement, que ce n’est jamais le cas.
Ce qu’on retrouve partout…
Tous les cryptosystèmes appliquant ces principes fonctionnent de la manière suivante :
- On dérive la clé primaire
- On applique une fonction de substitution
- On applique une fonction de permutation
- On revient à 1 et on repart pour un tour
Un peu de vocabulaire…
Dérivation de la clé primaire : Afin de respecter le premier principe, la clé primaire est dérivée successivement en plusieurs autres clés. Du coup, on aura bien une et une seule clé pour chaque passage.
S-box : Ce sont les Substitution-box qui assurent les fonctionnalités de substitution.
XOR : C’est le “OU” exclusif, une fonction très utilisée qui sera représentée sous la forme ![]() . Très simplement, cette relation renvoie 1 si deux éléments sont différents, 0 sinon. Ainsi :
. Très simplement, cette relation renvoie 1 si deux éléments sont différents, 0 sinon. Ainsi :
- 1
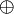 0 = 1
0 = 1 - 0
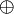 1 = 1
1 = 1 - 0
 0 = 0
0 = 0 - 1
 1 = 0
1 = 0
Un exemple, le DES
Bien ! Nous avons donc tous les éléments en main pour comprendre comment ça fonctionne. Maintenant petit jeu !!
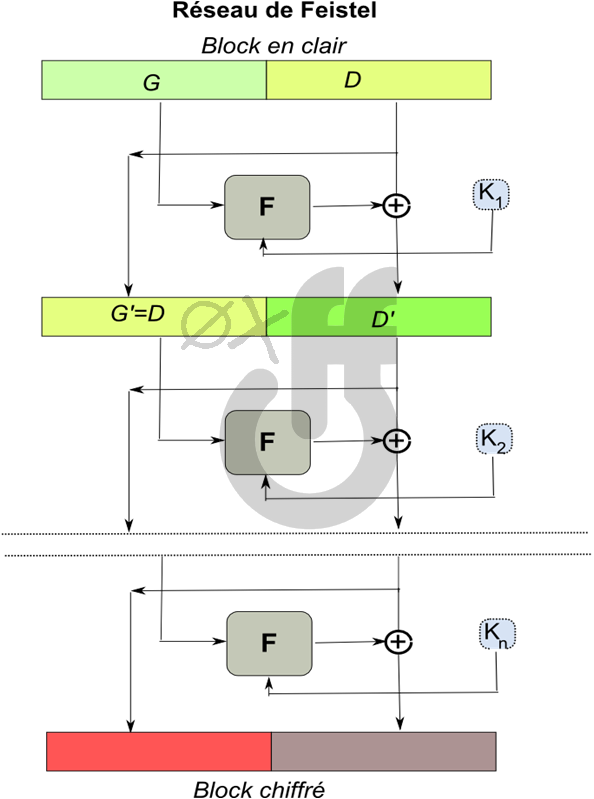
Dans le schéma de Feistel suivant essayez de repérer :
- Où se trouve les S-box ?
- Où s’opère la permutation ?
- Où sont les clés dérivées ?
Réponse :
- Où se trouve les S-box ? Au sein de la fonction “F”
- Où s’opère la permutation ? Dans ce schéma, c’est le passage gauche-droite
- Où sont les clés dérivées ? Ce sont les clés K1, K2, Kn
Regardons à présent cette fonction “F “ de plus près. Dans le cas du DES, elle ressemble à ceci :
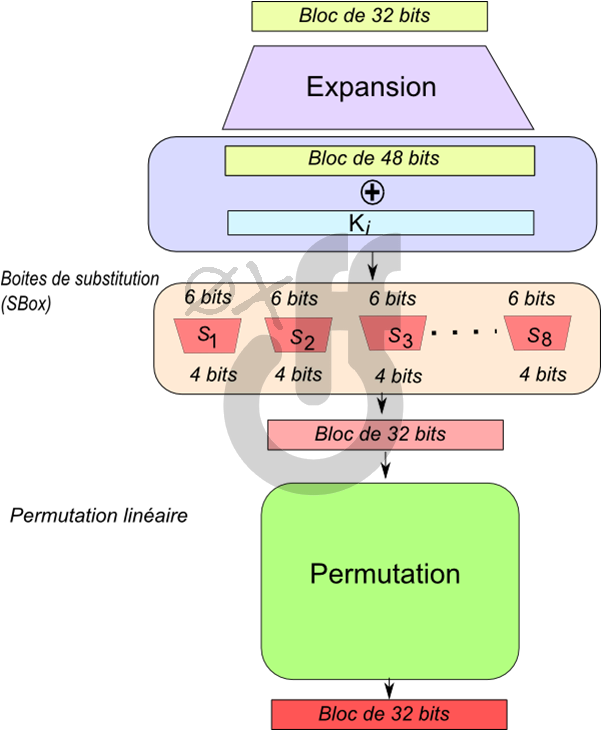
On retrouve bien nos S-box et un bloc de permutation au sein même de la fonction “F” . Mais sachant qu’une clé secrète K de DES fait 56 bits : quelle est la taille de Ki ? Et pourquoi ?
Et bien la taille de Ki est la même que la taille du bloc (48 bits) puisque l’on réalise une relation XOR entre le bloc de données et la clé. Ki est donc une clé dérivée de K au tour i (ou au “round i” comme on dit en Angleterre):
KDF(K, i) -> Ki
où KDF n’est pas un dictateur Libyen mais Key Derivation Function et “i” le numéro du tour (round).
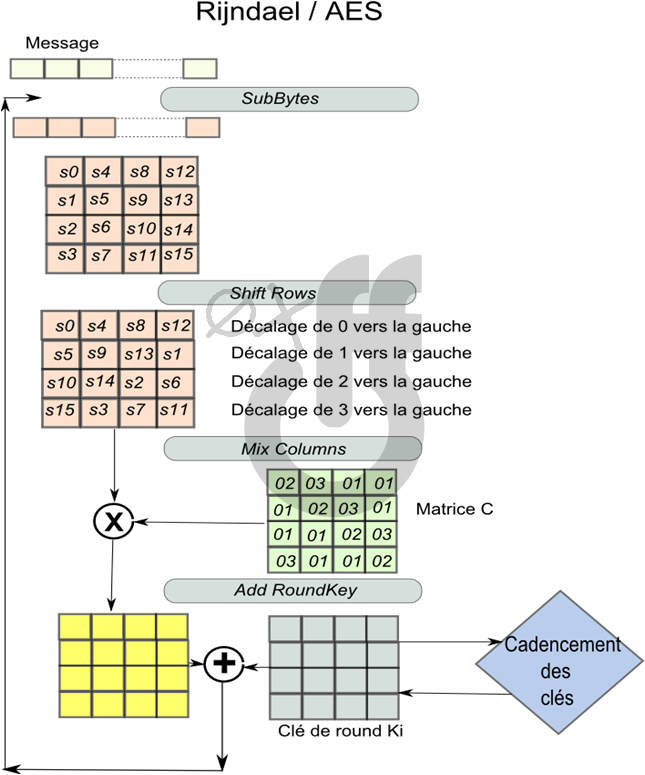
Nous venons de voir simplement (avouez-le) comment marche l’algorithme DES. Dites vous qu’il suffit de vous poser les mêmes questions sur n’importe quel cryptosystème pour le comprendre. Allez ! Je vous laisse un schéma simplifié de l’AES pour vous entraîner… Je suis comme ça moi, je donne !
Et si vous n’êtes pas certain de vos réponses, vous pouvez toujours m’écrire ou laisser un commentaire. ;)
Chiffrement par flot… Petit bateau !
En chiffrement symétrique, il existe 2 types d’échanges : par flot et par blocs chaînés. Les échanges par flot sont souvent utilisés pour les communications en flux continu, typiquement votre téléphone mobile grâce aux algorithme A5/1 ou A5/2. Et oui, nous utilisons chaque jour la cryptographie sans s’en rendre compte : c’est fou non ?!! Les échanges par blocs chaînés sont plus destinés aux blocs de données – surprenant ! – comme le chiffrement de n’importe quel document ou media.
Le chiffrement par flot.. Petit bateau !
Supposons que vous souhaitez communiquer avec Bob. Votre communication en clair est une suite de bits qui représente votre voix :
011010101
Dans le cas d’un chiffrement par flot vous possédez un générateur de clé pseudo-aléatoire, autrement appelé LFSR (Linear Feedback Shift Register). Pour chaque bit que vous allez envoyer, vous générez un bit de clé et vous XORez le tout.
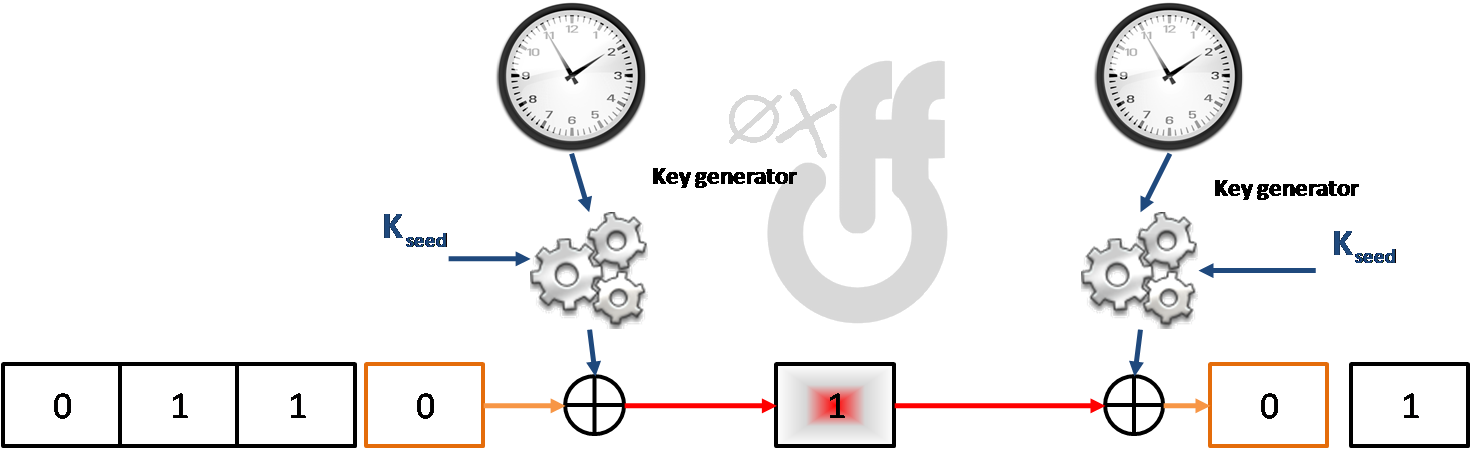
Vous comprenez aisément que si Bob n’a pas une horloge synchronisée avec Alice, il ne pourra rien déchiffrer. Damned !
Je ne parlerais pas ici des caractéristiques du polynôme de rétroaction du LFSR (périodicité, vecteur d’initialisation). Si vous souhaitez vraiment approfondir le sujet, j’écrirais un billet spécifique sur les générateurs pseudo-aléatoires… Enfin si vous voulez, parce que ça doit pas passionner tout le monde.
Le chiffrement par blocs chaînés
Le problème est le suivant : mes algorithmes de chiffrement n’acceptent que des clés de taille limitée de quelques centaines de bits. Je ne peux donc chiffrer que des blocs de taille limitée… Ce qui ne m’avance pas à grand chose pour chiffrer un film de plusieurs Go par exemple.
Du coup je vais utiliser des modes opératoires pour chaîner plein de blocs de bits.
Tous ces modes opératoires sont très bien détaillés dans cet article wikipedia. Après lecture de cette merveille de pédagogie wikipedestre, vous devez avoir remarqué que j’ai omis un objet cryptographique important, le vecteur d‘initialisation (IV).
L’IV permet d’ajouter un peu plus de confusion lors d’une cryptanalyse brute et méchante. Entre autres en offrant la possibilité d’obtenir deux messages chiffrés différents correspondant à un seul et unique message. Ainsi, lors d’un échange, Alice et Bob doivent partager :
- Un algorithme commun (ex : AES, 3DES)
- La clé secrète primaire (K)
- Le vecteur d’initialisation (IV)
… Bon évidemment c’est vrai et ce n’est pas vrai. Si l’on regarde de plus près les modèles CBC ou CFB, on voit que si on connait la clé mais pas l‘IV, seul le premier bloc va être faux…en gros vous n’allez pas pouvoir déchiffrer le titre de votre film, mais le reste sera clair comme de l’eau de roche.
Seuls les modèles OFB et CTR vous assurent que l’IV fait bien partie du secret (rappelez vous toujours la question “Où est le secret ?“) Et en bonus ! Ils permettent de pré-calculer les “clés dérivées” et donc d’être plus efficace lors d’échanges chiffrés.